Wie täusche ich bei vergleichenden Trenddarstellungen?

Das Beispiel aus Leibigers Dresdner Präsentation¹

Jürgen Leibiger gibt in seiner Präsenta­tion zum Ökonomie-Widerstreit¹ — wohl in redlicher Absicht — auf Seite 13 (ohne Quellenangabe) eine täu­schende Darstellung zur Lohnentwicklung mit einem sichtbar „starken Zurück­bleiben” der Real­lohn-Entwicklung 1948-2013 hinter dem Produk­tivitätsverlauf wieder:

Doch das suggerierte, so starke Auseinanderklaffen schien mir volkswirtschaft­lich nicht plausibel — da habe ich über die Kurven genauer nach­gedacht.

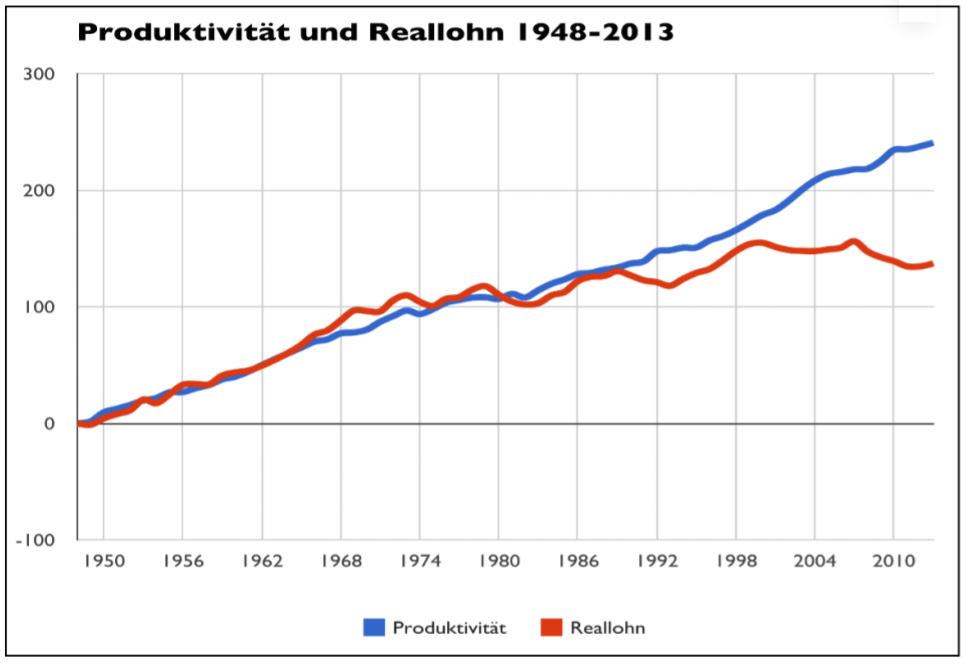
Ich erinnerte mich an einige Ratschläge aus dem Fach Statistik, besonders Hin­weise auf die Tricks, mit denen andere Aussagen nahegelegt werden sollen, als in den Daten stehen. Objektiv liegen statistische Daten nur im Original vor, z.B. als Zeitreihen in Excel-Tabellen. In unserem Beispiel handelt es sich um die Pro­duktivitätsreihe, die Nominallohnreihe und eine Preisindexreihe. Entgegen ver­breiteter Ansicht ist jede daraus gewonnene Grafik in irgendeiner Weise mani­pulativ. Hier sind vier Tricks:

Bei Reallöhnen besteht der erste Trick in der Auswahl des Anfangsdatums, um damit die Reallohnreihe zu errechnen. Je nachdem, ob an dieser Stelle der Nomi­nallohnreihe eine Delle nach unten oder eine Delle nach oben getroffen wird, sind auch die weiteren Reallohnangaben überhöht oder unterschätzt.

Der zweite Trick besteht darin, an der senkrechten Achse einfach die Kurven bei ihrem niedrigsten Wert beginnen zu lassen (ohne Kennzeichnung, dass da ein unterer Bereich weggelassen wurde) oder umgekehrt bei einer unberechtig­ten Null zu starten. Natürlich kann der Reallohn 1948 nicht 0 gewesen sein und auch die Pro­duktivität nicht 0. Stellen wir uns die Grafik mit Vorgeschichte mal fiktiv (und vereinfacht) so vor:   _{Abb. 2}

Schon sieht das Auseinanderklaffen relativ nicht mehr ganz so stark aus.

Ein dritter Trick ist die Transformation in einen einzigen Wertebereich. Da zu jedem Zeitpunkt die Produktivität deutlich über dem entsprechenden Nominal­lohn liegen muss (kapitalistische Überlebensbedingung) und der Anfangswert der Reallohnreihe genau gleich dem ersten Nominallohn sein muss, sollte der Wertebereich der Reallöhne unter dem der Produktivitäten liegen. Dann kann der Anfangswert der Reallohnkurve aber nicht auf gleicher Höhe wie der An­fangswert der Produktivitätskurve liegen. Sowohl in Abb. 1 wie auch in Abb. 5 wurde der Wertebereich der Reallöhne in den Wertebereich der Produktivitäten entsprechend hoch transformiert — eine klare Manipulation.

Aber der Trick mit der gemeinsamen senkrechten Skala ist noch suggestiver.

Das Prinzip

Wie das funktioniert, möchte ich an einem einfachen Beispiel zeigen, das hypo­thetische Preise für Gold und Silber vergleicht. Wir wollen hier annehmen, der Goldpreis sei immer genau doppelt so hoch gewesen wie der Silberpreis, bei gleichmäßi­ger Entwicklung. Dann erhalten wir mit dem Ein-Skalen-Trick:

    _{Abb. 3:}

Korrektur an einem anderen Beispiel

Die Quelle für Leibigers Abbildung konnte ich nicht finden, aber ich fand eine ähnliche Grafik²:     _{Abb. 5:}

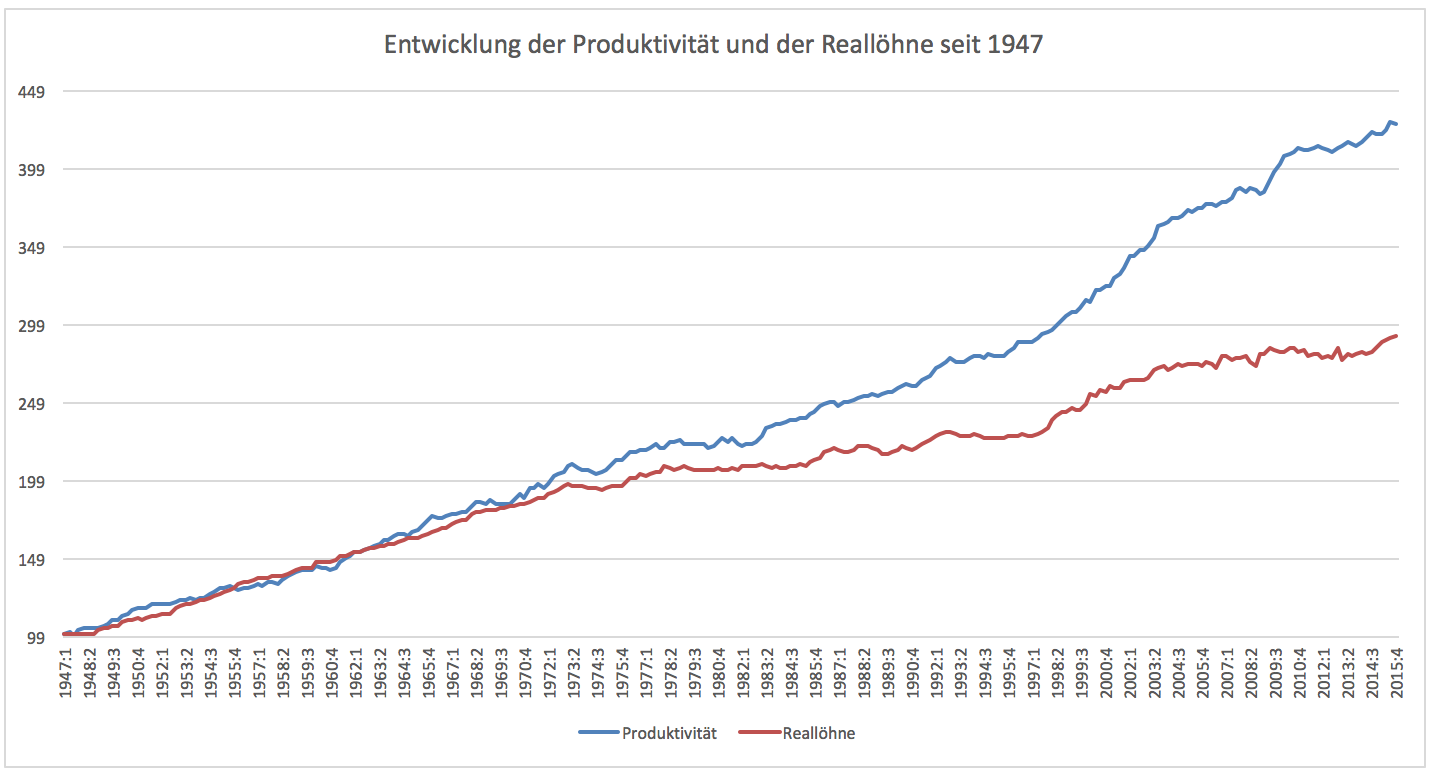
Ich habe mal die Reallohn-Kurve angepasst, indem ich die Endpunkte aufeinan­dergelegt und die rechte Skala angeglichen habe. Es war stundenlange Ar­beit: Manuelles Herausarbeiten je eines Bildes nur mit der blauen bzw. nur mit der roten Kurve, Einfügen der linken Skala auch rechts im roten Bild, Verzer­ren des roten Bildes, bis der Endpunkt die Höhe des blauen Endpunkts im Ori­ginal erreicht, und schließlich transparentes Zusammenkopieren der beiden Bilder.

_{Abb. 6:}

Schon lassen sich die gleichen zugrundeliegenden Daten (die gleichen Zah­lenreihen für Produktivität und Reallöhne, und natürlich unsichtbar auch für Nominallöhne und Preisindizes) ganz anders in­ter­pretieren: „Die Reallöhne waren der Produktivität davongeeilt und haben sich nun wieder angeglichen.” Gültig bleibt die Aussage: „Die Reallöhne stie­gen zuletzt relativ zur Produkti­vität weniger stark”, unregelmäßig, fast unmerklich.

Doch auch das ist fehlerhaft suggestiv. Die Endpunkte beider Kurven sind nicht repräsentativ für den durchschnittlichen Verlauf. Man müsste bei­de Durch­schnitte auf gleiche Höhe legen und eine entsprechende rechte Skala bilden. Da ich über die Daten selbst nicht ver­fü­ge, kann ich das hier nicht zeigen. Auch müsste ich nach der Skalen-Eigen­schaft fragen: Muss ich das arithmetische Mittel oder das geometri­sche Mittel neh­men? Doch welcher Statistiker macht sich schon diese Arbeit?

Zweifelt „sich öffnende Scheren” in populären Statistiken ruhig mal an — aber schließt sie auch nicht ganz aus! Möglich wären sie schon — aber seltener.

---